dev-resources.site
for different kinds of informations.
ZKP Series #3 [Finite fields & Modular Arithmetic ]
Computers have a history of finding it difficult to handle floating point numbers ; in simple terms, decimals but more so infinite decimals
If this is difficult to visualize you are not alone I am a visual learner so I have placed
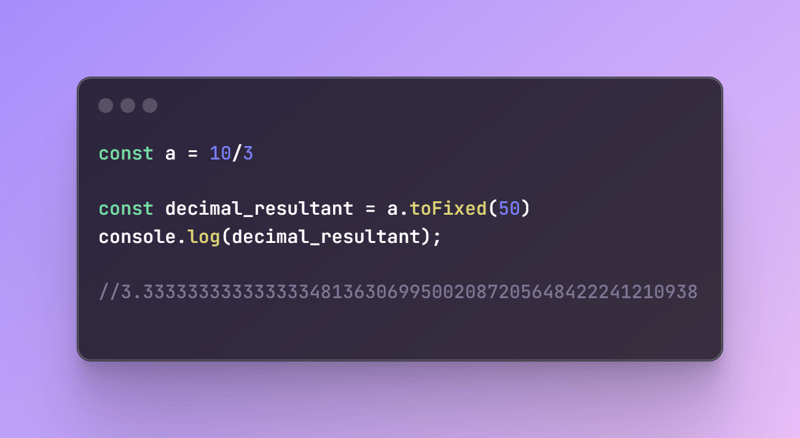
const a = 10/3
const decimal_resultant = a.toFixed(50)
console.log(decimal_resultant);
#Click the link below and please copy and paste the code here to see the results of this fraction or decimal
https://www.tutorialspoint.com/execute_nodejs_online.php
This was the value we got from doing the fraction operation 3.333333333333333481363069950020872056484222412109375000000000.
In short, we get re-occurring 3's after the .(dot) and then we get some random numbers and give up with zeros
This means we lose some precision with such numbers.
The Number System.
With the precision issue in mind, we need to understand the number system.
Understanding the Number System
To tackle this precision issue, we must delve into the underlying number system. Here's a breakdown:
Natural Numbers (ℕ): These are the counting numbers, starting from 1 and continuing indefinitely. While some include zero in this set, others exclude it.
Integers (ℤ): The set of all whole numbers, including both positive and negative integers.
Rational Numbers (ℚ): Any number that can be expressed as the quotient or fraction of two integers, where the denominator is not zero.
Real Numbers (ℝ): This encompasses all rational and irrational numbers, essentially covering the entire number line.
Complex Numbers (ℂ): This set includes numbers in the form of a + bi, where "a" and "b" are real numbers, and "i" represents the imaginary unit.
These number systems especially when used in cryptography cause issues due to computer architecture. We are going to borrow its some properties like arithmetic operations
Addition: 6 + 30 = 36
Substraction: 90 - 30 = 60
Multiplcation :
Division : 10/3 = .. our problem 3.333333333333333481363069950020872056484222412109375000000000.
what is zero = any number added to zero would give the same number that is zero n+0 =n
what are negatives = n+(-n) = 0
underlaying that issue and see if we can create a solution.
We need a number system that is
- Would be primary based on whole numbers eg: 0, 1, 2, 3, 5,....
- Only limited number of whole numbers [finite not infinite]
- Be able to add all arithmetic operations you can do with our known number system eg of arithmetic operations include multiplication, addition , subtraction, division , exponentials..
Modulo Arithemetic
In the realm of modulo arithmetic, where numbers wrap around like a circular clock face, understanding addition and subtraction is essential for navigating numerical progression. Let's delve into modulo addition and subtraction through illustrative examples.
Modulo Addition
Example 1: Modulo Addition (Mod 12)
Let's visualize the expression 8 + 5 (mod 12):
Modulo Addition Example 1
We begin at the number 8 and proceed five steps clockwise on the modulo clock. As we reach 12, the sequence wraps around, resulting in the sum 1 (8 + 5 ≡ 1 mod 12).
Example 2: Modulo Addition (Mod 7)
Now, let's explore 4 + 6 (mod 7):
Modulo Addition Example 2
Following the same principle, we advance four steps from 4 on the modulo clock. The outcome, 3 (4 + 6 ≡ 3 mod 7), showcases the cyclical nature of modulo addition within our finite integer set.
Modulo Subtraction/ Additive Inverse
Example 1: Modulo Subtraction (Mod 12)
Consider the expression 3 - 9 (mod 12):
Modulo Subtraction Example 1
To calculate negative modulo, we use the formula: -a mod b = b - (a mod b).
For -6 mod 12:
- First, we find 6 mod 12, which equals 6.
- Then, we apply the formula: -6 mod 12 = 12 - (6 mod 12) = 12 - 6 = 6.
** Example 2: Modulo Subtraction (Mod 7)**
Let's navigate 6 - 4 (mod 7):
Modulo Subtraction Example 2
Starting at 6, we backtrack four steps counterclockwise on the modulo clock. The result, 2 (6 - 4 ≡ 2 mod 7), illustrates the reverse traversal characteristic of modulo subtraction within our finite integer set.
Through these examples, we gain insights into the dynamics of modulo arithmetic, paving the way for a deeper understanding of numerical progression and computational algorithms.
Multiplication with Modular Arithmetic:
Example: Multiplication with Modulo (Mod 12)
Multiplication is consecutive addition
Consider the expression 3 * 4 (mod 12):
Modulo Multiplication Example
We multiply 3 by 4 and then find the remainder when divided by 12. The result, 0 (3 * 4 ≡ 0 mod 12), showcases the structured nature of modulo multiplication within our finite integer set.
The Multiplicative Identity
Within modulo arithmetic, the number 1 serves as the multiplicative identity, anchoring numerical operations with unity and stability.
Example: Multiplicative Identity (Mod 7)
Let's examine the expression 5 * 1 (mod 7):
Multiplicative Identity Example link_to_image_6
Multiplying any number by 1 within the modulo 7 system retains the original value, illustrating the fundamental role of the multiplicative identity in maintaining numerical integrity.
The Multiplicative Inverse
In modulo arithmetic, the concept of multiplicative inverses enables division-like operations within finite fields, enhancing computational versatility.
Example: Multiplicative Inverse (Mod 13)
Consider the expression 5 * 8 (mod 13), seeking the multiplicative inverse of 5:
Multiplicative Inverse Example link_to_image_7
By finding the number that, when multiplied by 5, yields 1 (mod 13), we identify the multiplicative inverse of 5 as 8. This demonstrates the pivotal role of multiplicative inverses in modulo arithmetic.
The Case of 3 in Mod 12
| Expression | Result |
|---|---|
| 3 x 1 | 3 |
| 3 x 2 | 6 |
| 3 x 3 | 9 |
| 3 x 4 | 0 |
| 3 x 5 | 3 |
| 3 x 6 | 6 |
| 3 x 7 | 9 |
| 3 x 8 | 0 |
| 3 x 9 | 3 |
| 3 x 10 | 6 |
| 3 x 11 | 9 |
| 3 x 12 | 0 |
Problems with Multiples of 3 (Mod 12):
- Limited Reach: Not every number can be reached from a multiple of 3 within mod 12 arithmetic.
- Cyclic Results: The results exhibit cyclical patterns, leading to duplicity paradoxes.
- Ridiculous Results: The presence of 0 as a result in the sequence raises questions about the logical consistency of the arithmetic.
The Good Case of 5 in Mod 12
| Expression | Result |
|---|---|
| 5 x 1 | 5 |
| 5 x 2 | 10 |
| 5 x 3 | 3 |
| 5 x 4 | 8 |
| 5 x 5 | 1 |
| 5 x 6 | 11 |
| 5 x 7 | 4 |
| 5 x 8 | 9 |
| 5 x 9 | 2 |
| 5 x 10 | 7 |
| 5 x 11 | 0 |
| 5 x 12 | 0 |
Advantages of Multiples of 5 (Mod 12):
- Complete Reach: Every number can be reached from a multiple of 5 within mod 12 arithmetic.
- No Cyclic Results: The results exhibit no cyclic patterns, ensuring logical consistency and avoiding duplicity paradoxes.
- Logical Results: The results maintain logical coherence, with no unexpected or absurd outcomes.
Utilizing Prime Numbers in Mod Arithmetic
In the examples above, using 5 (a prime number) as the modulus in modulo arithmetic yields favorable outcomes, leading to a well-defined and structured sequence of results. This concept extends to prime fields, where the modulus is a prime number.
When a prime number is utilized as the modulus (e.g., mod 5), the resulting arithmetic operations exhibit enhanced properties, including complete reachability, absence of cyclic patterns, and logical consistency. Hence, employing prime numbers as moduli in arithmetic operations leads to more robust and reliable outcomes, paving the way for the establishment of prime fields in computational frameworks.
Power Operations
Exponentiation unfolds seamlessly within modulo arithmetic, leveraging consecutive multiplication to navigate numerical landscapes with precision and efficiency.
Example: Exponentiation (Mod 11)
Let's explore the expression 3^4 (mod 11):
Exponentiation Example
By consecutively multiplying 3 four times and finding the remainder when divided by 11, we arrive at the result, 4 (3^4 ≡ 4 mod 11), exemplifying the well-defined nature of exponentiation within finite fields.
Defining Generators (Mod p)
Generators play a pivotal role in modulo arithmetic, offering a structured framework for numerical exploration and algorithmic development. A member element whose power can reach every element in a finite field is called a generator (or primitive element).
A key property of generators is that raising them to the power of (p-1) yields 1: g^(p-1) = 1, where 'g' is the generator and 'p' is the prime modulus.
Consider the integer set {1, 2, 3, ..., p-1} within modulo p arithmetic. A generator, such as 3, possesses the unique property of generating all elements of the set through exponentiation:
| Power | Result (3^power mod p) |
|---|---|
| 0 | 1 |
| 1 | 3 |
| 2 | 9 |
| 3 | 10 |
| 4 | 13 |
| 5 | 5 |
| 6 | 15 |
| 7 | 11 |
| 8 | 16 |
| 9 | 14 |
| 10 | 8 |
| 11 | 7 |
| 12 | 4 |
| 13 | 12 |
| 14 | 6 |
| 15 | 2 |
| p-1 | 1 |
By raising the generator 3 to various powers, we traverse through the entire integer set within the modulo p system, showcasing the versatility and power of generators in modulo arithmetic.
Through these examples and properties, we unravel the intricacies of generators in modulo arithmetic, illustrating their significance in computational frameworks and cryptographic protocols.
Modulo Identities
| Law | Expression | Equivalent |
|---|---|---|
| Additive Distribution | (a + b + c) mod m | (a mod m) + (b mod m) + (c mod m) |
| Multiplicative Distribution | (a ⋅ b) mod m | [(a mod m) ⋅ (b mod m)] mod m |
Prime Field vs. Non-Prime Field: Arithmetic Operation Comparison
| Property | Prime Field | Non-Prime Field |
|---|---|---|
| Modulus | Prime number (e.g., 17, 23, 29) | Non-prime number (e.g., 12, 15, 20) |
| Additive Operation | Modular addition | Traditional addition |
| Subtractive Operation | Modular subtraction | Traditional subtraction |
| Multiplicative Operation | Modular multiplication | Traditional multiplication |
| Division-like Operation | Modular division (using multiplicative inverses) | Division (may not be well-defined) |
| Exponential Operation | Consecutive multiplication with modulo arithmetic | Conventional repeated multiplication |
| Resulting Properties | ||
| - Completeness | All elements of the field are generated | Some elements may not be reachable |
| - Predictability | Well-defined, consistent outcomes | Results may vary, leading to ambiguity |
| - Efficiency | Structured operations, efficient computation | Repetitive operations, potentially less efficient |
| - Stability | Logical, coherent results | Potential for inconsistency and unpredictability |
In a prime field, arithmetic operations leverage the modulus of a prime number, ensuring completeness, predictability, efficiency, and stability. Modular arithmetic facilitates well-defined outcomes for addition, subtraction, multiplication, and division-like operations, with the aid of a generator for exponentiation.
Conversely, in a non-prime field, arithmetic operations may lack the structured properties of a prime field. The absence of a prime modulus and generator can lead to incomplete reachability, varied results, and potentially less efficient and stable computation. Traditional arithmetic operations may not be well-defined or may exhibit ambiguity and unpredictability.
Next Part would be focused on Set Theory & Group Theory . We are doing this to set the tone for Elliptic Curve Cryptography
Featured ones: